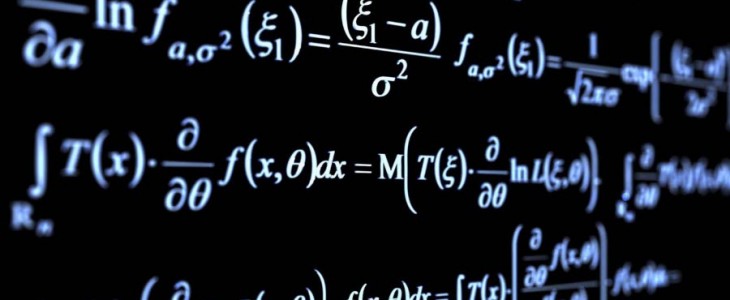Как использовать среднеквадратическое отклонение в ставках?

Услышав термин «среднеквадратические отклонение», многие капперы вспомнили старшие классы школы и то, как они не любили уроки алгебры. Кто-то может вспомнит даже момент, как в адрес учителя математики были произнесены слов: «А как мне это пригодится в жизни?». Ирония судьбы – среднеквадратическое отклонение настигло вас в ставках на спорт. Ведь с помощью этого показателя можно составлять прогнозы на матчи.

Что собой представляет среднеквадратическое отклонение? В теории вероятностей и статистике – это наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок. Это значение показывает, есть ли связь между определенными данными в выборками и какая она (линейная, например).

Использование распределения Пуассона

Например, известно, что очень многие бетторы пользуются методом распределения Пуассона для прогнозирования общего количества голов, а также результативности отдельных команд в футбольном матче. И в этом статистическом распределении используется один исходный параметр, от которого очень сильно зависит итоговый результат – средняя величина. Это дискретное распределение с выходными значениями в виде целых чисел.

Модель Пусанно скорее подойдет для оценки вероятности взятия ворот вообще. Этот метод не слишком рабостопобен, когда необходимо определить вероятность на каком-то небольшому временном промежутке. Скажем, вы хотите узнать, какие шансы команды на взятие в ворот в первые 15 минут матча. Для этого вам придется менять выборку данных и пересчитывать все заоново.

Стандартное распределение (его называют еще распределением колоколообразной формы или распределением Гаусса) – еще один статистический инструмент, который часто используется игроками в букмекерских конторах. Она имеет свои отличи в сравнении с тем, что предлагает метод Пуассона. Например, здесь за основу берется сразу два ключевых параметра – это средняя величина, а также среднеквадратическое отклонение.

Расчет количества забитых мячей на примере чемпионата Англии

Для примера возьмем результаты одной из самых популярных футбольных лиг в мире — АПЛ. Можно предположить, что для разницы голов в каждом матче действует закон гауссового распределения. Разница голов – это количество голов хозяев минус количество мячей, которые были забитые гостевыми командами. В свою очередь значение ноль отвечает такому исходу как ничья.

В качестве выборки используем результаты английском премьер лиги в сезоне 2013–2014 гг.

• Самую результативную игру у себя на родном стадионе показали футболисты из Манчестер Сити, которые одолели гостей из Норвича со счетом 7-0;.
• В то время как самый большой счет с победой гостевой команды, был зафиксирован во встрече Ливерпуль Тоттенхэм – 0:5.
• Средняя разница голов по всему сезону составила 0,3789 (медиана и мода = 0).
• Величина среднеквадратического отклонения составила 1,9188.

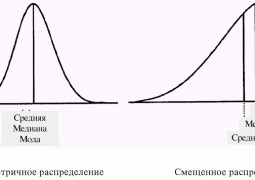
На основании рассчитанных показателей и полученных данных можно сделать несколько важных выводов. Наиболее частым показателем при подсчете разницы голов является ничейный результат. Достигается практически симметрическое распределение с перевесом в сторону побед на своем поле. Однако эта статья посвящена в первую очередь среднеквадратическому отклонению.

Работа со среднеквадратическим отклонением.

Для формирования типовой кривой нормального распределения используются два параметра (средняя величина и среднеквадратическое отклонение). При этом одно среднеквадратическое отклонение от средней величины относится примерно к 68 % распределения, а 2 среднеквадратических отклонения – к 95 %.

В этом случае ожидается, что 68 % игр будут завершены с показателями от -1,5399 до 2,2977 гола (т. е., 0,3789 + /-1,9188). Для непрерывной кривой действуют свои ограничения: недопустимой становится разница голов с показателем -1,5399.

Чтобы оценить победы на своем поле с помощью разницы голов, целое значение 1 можно заменить на значение из диапазона от 0,5 до 1,5. Затем каждое значение можно сравнить со средней величиной с учетом среднеквадратических отклонений.

В результате появляется прекрасная возможность заново составить модель нормального распределения (см. рисунок). В этом случае необходимо выбрать область оранжевого цвета. Вот что можно сказать о зоне с синим цветом: существует вероятность в размере 52,15%, что будет забито менее одного мяча (либо с эквивалентным уровнем менее 0,5 гола).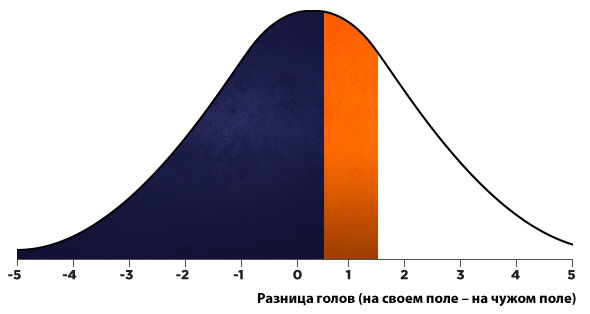

Подробный расчет не требуется, но он может быть выполнен с помощью большинства программ для работы с электронными таблицами, например в MS Excel: =НОРМ.РАСП(0,5;0,3789;1,9188;1). Аналогичным образом можно рассчитать вероятность голов ниже показателя 1,5. Она находится на уровне 72,05 % Таким образом, ожидаемая разница между этими двумя значениями составляет 19,53 %.

По итогам оценки 74,22 матча из 380 завершились бы победой на своем поле с разницей всего в один гол. И на самом деле, 75 матчей в сезоне 2013-2014 закончились с указанным результатом. Как видите, полученный показатель очень близок к фактическому значению.

Моделируя те самые действия для всех случаев с разницей голов, можно сравнивать фактическое и предположительное количество матчей, завершившихся с различными показателями разницы голов.

В нижеприведенной таблице указано минимальное расхождение – в этом случае нормальное распределение подобрано правильно. Проверку нормальности распределения можно выполнить различными способами. Описанное распределение успешно применяется для анализа статистики турнира Английской премьер-лиги в сезоне 2013-2014.

Допустим, что распределение подходит для оценки матчей текущего сезона какого-то футбольного чемпионата Англиии. Капперы, которые размещает ставки с учетом разницы голов, может пригодиться информация о вероятности выигрыша команды хозяев поля с разницей не менее чем в один гол в рамках Премьер-Лиги. Рассчитать значение можно по следующей формуле: 100 % – 52,52 % = 47,48 %.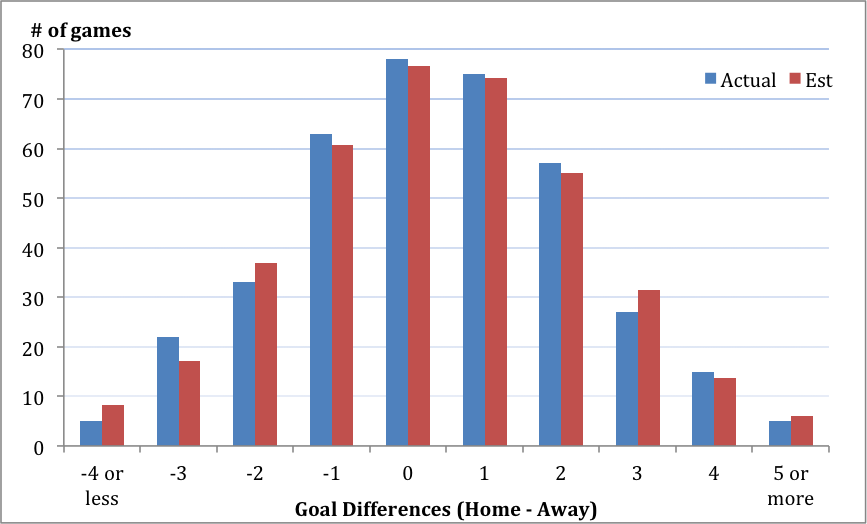

Безусловно, рассчитанный нами показатель применим в целом к результатам матчей Премьер-лиги, а не к достижениям отдельных команд. Игрокам следует брать в расчет игры команд, на которые они ставят, а не ориентироваться на средний показатель по всему чемпионату. Вы можете взять любую другу лигу или команду и рассчитать для них свое значение.

В заключение следует добавить, что среднеквадратическое отклонение – это не просто мера разброса числовых данных (чем больше значение, тем сильнее разброс в группе). Это также важный параметр для расчета вероятности, что крайне полезно для игроков, размещающих ставки на спортивные события. Применить это знание на практики не так просто как вам кажется. Нужно внимательно обновлять все данные и вести параллельный расчет (если вы ставите на несколько команд сразу). Только тогда можно рассчитывать на определенную точность, которая в итоге принесет вам желаемую прибыль. Попробовать стоит – статистика не должна работать «на глаз», она должна «подсказывать» вам фактами.