Обманный эффект среднего значения в ставках

Практически в любой отрасли человеческой деятельности среднее используют средние значения. Это касается экономики, финансов, производства, строительства. Среднее значение хорошо известно и бетторам, как один из вариантов оценки данных при размещении ставок. Только так ли ценен этот показатель на самом деле? Эта статья покажет, почему мода и медиана – куда более важные и красноречивые значения.

Использование среднего значения и возможных последствия

Рассчитать среднее значение довольно просто. Достаточно просто посчитать сумму чего-то (например, забитых мячей) и поделить на количество (например, матчей). Короткая операция дает игроку, как он считает, полезное значение, которое можно использовать при анализе или осуществлении ставки. Вроде бы все выглядит логично. Вы хотите поставить на рынок тоталов в каком-то отдельном матче. Тогда вы беретесь изучать результативность команд, которые берут участие в поединке и устанавливаете среднее значение. И на этом основании и делаете свою ставку. Но у этого способа есть немало изъянов, которые и могут исказить реальное положение дел. Ведь среднее значение только дает общее представление о количестве забитых мячей. Но упускается то, за счет чего было сформировано это значение.

Для примера можно сравнить результативность чемпионата Испании (Ла Лига) и английском премьер-лиги в сезоне 2013/2014. Так вот, в английской лиге забивали в среднем 2,77 гола за матч, а в испанской – 2,75. Какой же с этого можно сделать вывод? Ну, прежде всего, что чемпионат Англии результативнее. И этот вывод правильный. Но точно также на основании данной информации многие могут предположить, что в премьер-лиге чаще пробивался тотал 2,5. Вот тут и вступает в силу изъян среднего значения. На самом деле, в 52,7% матчей в Ла Лиге забивалось больше 2,5 мячей, в то время как в чемпионате Англии этот показатель установился на уровне 51,6%.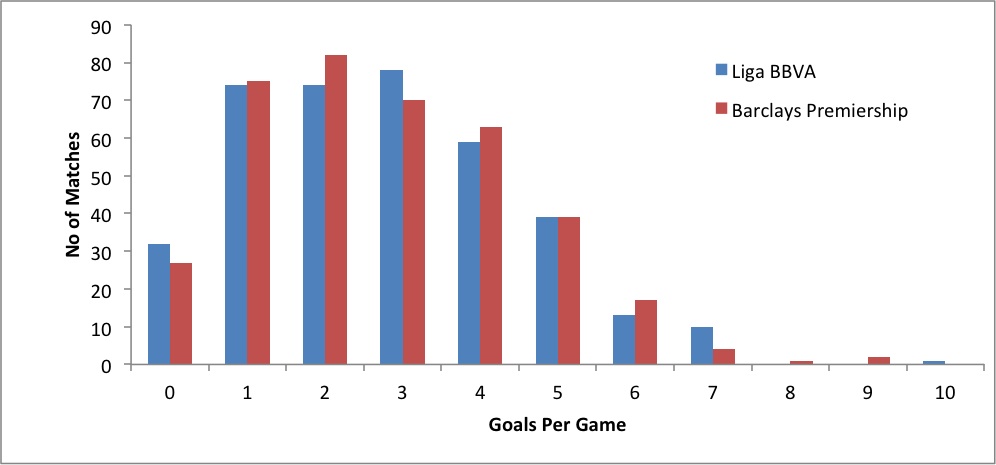

Наглядное распределение результативности по отдельным матчам можно наблюдать на примере диаграммы. Например, здесь можно увидеть, что в чемпионате Испании гораздо чаще игры заканчивались с тремя забитыми мячами. Это во многом и определило общий процент матчей с ТБ 2,5.

Как видите, среднее значение не совсем точно передает реальное положение дел. И на рынках тоталов или фор оценка с помощью этого показателя несколько неэффективна. Особенно если вы ставите на международный футбол. Мало того, что там у команд достаточно нестабильные составы и игровая форма, там и разрыв в классе игроков частенько бывает большим. В итоге одна пару встреч со сборными уровня Сан-Марино или Гибралтара могут существенно исказить общие показатели. Поэтому не стоит использовать среднее значение при подобных ставках.

Если среднее значение неэффективно, то что же тогда использовать? На самом деле, у этого показателя есть хорошие альтернативы – это мода и медиана. Эти значения активно используются в статистике, теории вероятностей и различных оценках. С их помощью можно получить более красноречивую информацию.

Давайте рассмотрим особенности этих значений. Для этого проанализируем три набора чисел – А, Б, В. Среднее значение каждого из них составляет 5. Но даже невооруженным взглядом видно, что наборы чисел серьезно отличается друг от друга.

•        Набор А: 4, 5, 5, 5, 6.
•        Набор Б: 3, 4, 4, 4, 10.
•        Набор В: 3, 4, 5, 6, 7.

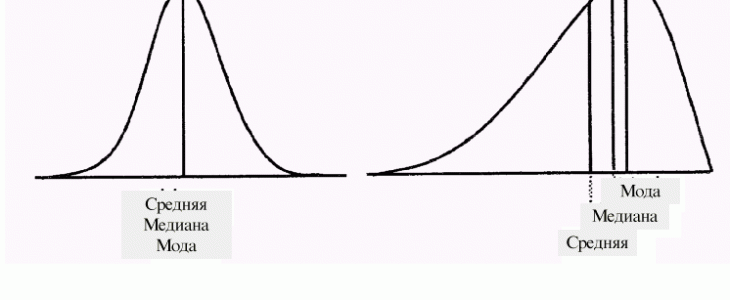
Для начала остановимся на наборе А. Его можно назвать более мене равномерным или скорее симметричным. Среди 5 значений есть сразу 3 одинаковых и 2, которые лишь на единицу ниже среднего значения. То есть они отличается от этого показателя на одно и то же значение (1), только с разными знаками. Среднее значение – это идеальный вариант при наличии симметричного распределения, когда значения переменных возникают с одинаковой частотой в начале и в конце указанного набора. Среднее значение приведено посередине набора.

А теперь присмотритесь до набора Б. Обратите внимание, что в этой подборке, есть только одно число, которое превышает среднее значение – это 10. Такое распределение можно назвать несимметричным. А теперь представьте, что это результативность матчей хоккейных команд. Вы думаете над тем, стоит ли ставить на ТБ 4,5. Какая из подборок подойдет для этого больше? Конечно же, первая, так как там сразу 5 раз вы увидели превышение этого тотала. А во второй подборке это произошло всего раз. При этом среднее значение этих наборов идентичное.

Как мы уже отмечали выше, у среднего значения есть альтернативы – это мода и медиана. Эти значения могут показать реальную «значимость» среднего показателя. Медиана – это значение, которое находится в «центре» определенной подборки. Например, в последовательности 1,2,3 – это будет 2, точно также как и в последовательности 1, 2, 2, 4. Если говорить за наборы А и Б, то тут медианы – это 5 и 4 соответственно. Мода – это наиболее часто встречающееся значение – 5 и 4 соответственно.

Если последовательность симметричная, то мода и медиана всегда будут принимать одно значение. Определить симметричность той или иной подборки довольно просто. Вам нужно отнять от среднего показателя «крайние» значения (самое большое и самое меньшее). Если результат будет совпадать по модулю, то последовательность симметричная.

Теперь обратите внимание на последовательность В. Первое, что вам бросилось в глаза – это равномерное возрастание элементов последовательности. Но, как и подборка А, набор В является симметричным. Среднее значение -5. 3-5=-2 и 7-5 = 2. 2 и -2 по модулю равны. При этом наборы А и В серьезно отличаются по своим элементам.

Поскольку в итоге мы получаем среднее значение, равное 5, это среднее значение больше подходит для набора А, поскольку он содержит больше чисел, более близких к среднему арифметическому. Разница между двумя последовательностями состоит в разбросе значений в группе. Поэтому необходимо определить разброс значений.

Действительно, между элементами есть разница. Но существуют также другие показатели, которые могут характеризовать последовательность. Речь идет о размахе и среднеквадратическом отклонении. Первый показатель представляет собой разницу между максимальным и минимальным значением в наборе. Среднеквадратическое отклонение рассчитывает более сложно и используется для того, чтобы изучить связь между различными элементами выборки. При его расчете учитывается дисперсия, среднее значение, а также максимумы и минимумы последовательностей. .

Величина размаха для наборов А и В составляет 2 и 4, а среднеквадратическое отклонение – 0,71 и 1,58 (соответственно). Обе величины больше для набора В – это еще один показатель того, что в последней группе наблюдается более существенное различие. То есть набор А – куда более «надежный» и объективный, если можно выразиться такими словами.

Вывод

Отказываться от среднего значения не нужно. Просто необходимо понимать то, как он формируется и насколько он может искажать реальное положение дел. Если игрок научится понимать эти вещи, то он ограничит количество обидных ошибок при оценке или анализе различных спортивных событий. Имея в запасе знания о моде, медиане и других статистических показателя, вы значительно улучшите свой статистический анализ.